Wireless Lights. Remotely Controllable, Cheaper to Run, Longer-Lasting.

Wireless lights are an exciting option for lighting your home. Standard-fitting ‘Smart light bulbs’, the product of LED (Light Emitting Diode) lighting and wireless technology, are setting a new standard in lighting control and power saving.

Wireless LED lights can bring you three main benefits

You can control them easily with a remote control, or sometimes with a Smartphone with a suitable app
They last much longer than a conventional bulb, typically 50 times longer than incandescent bulbs
Wireless LED lights are much less expensive to run as they don't generate much heat - wasting power that you have to pay for

You can turn an individual wireless light bulb on or off or dim it... you choose.

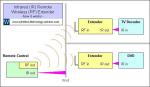
Remote control

You can control wireless lights...

Inside your home - with a short-range remote controller, or with your Smartphone loaded with suitable application software (app)
Outside your home - via the Internet, with a computer, tablet or Smartphone with app

...each has an address

Longer lasting wireless lights

LED lights live much longer than incandescent or compact fluorescent bulbs

One manufacturer specifies the life of its LED light as 52,000 hours
Conventional incandescent bulbs typically live about 1000 hours
Compact fluorescent bulbs may live about 10,000 hours.

So these lights live about 50 times as long as an incandescent bulb.

LED lights use totally different technology to that used in incandescent or compact fluorescent lights

A LED is an electronic component – a semiconductor diode
Predictable – the manufacturing process is tightly controlled
Efficient – doesn’t waste as much electricity (by producing heat)
A LED is more robust than the filament in an incandescent bulb

Less expensive to run

The cost of running a wireless light bulb, or any electric light, depends on how much electric power it uses

Power is the ‘amount of energy’ that the light uses every second
A 60 Watt bulb uses 60 Joules of electrical energy every second
An 8 Watt bulb uses only 8 Joules of electrical energy every second
When you dim them they use even less power

If there were such a thing as a perfect light, it would convert all of the electrical energy it used into light energy. But there’s no such thing as the perfect light. Unfortunately, lights also convert some of the electrical energy they use into heat, and while the heat isn’t wasted if the room is cold, we really want the light, not the heat.

an incandescent bulb converts most of the energy it uses into heat
only a small amount is converted into light (that’s very inefficient)
on the other hand, LED lights are relatively efficient.

Look at the print on the packaging of a compact fluorescent or LED light bulb.

You may see something like ‘8W… equivalent to 60W’.

This means that for the same amount of light, while the standard incandescent bulb uses 60 Watts of electric power, the LED light only uses 8 Watts…

seven and a half times less power for the same amount of light, so…
seven and a half times cheaper to run.

Easy to install and set up

The first of the wireless lights available is the award-winning Insteon. This has a standard medium Edison screw-in base and fits just like an ordinary bulb. So far only a 120VAC 60Hz version is available, though they should quickly become available in other voltages and with other fittings.

A wireless light bulb is slightly bigger than a conventional bulb, so take this into account if you want to use one where space is limited.

Setup appears to be straightforward.

When you add a new wireless light bulb, it ‘tells’ the controller ‘I’m a new bulb, number xxx, please include me in your network’. The controller then links to it and adds it to the network along with any other wireless bulbs.

Here are ten interesting and useful wireless products